『shuTOMO9月号』連動企画　数学は、フェアな学問です（１）

早稲田大学高等学院・中学部 学院長 武沢護先生（中央）
洗足学園中学高等学校 学力形成部（進路担当） 平井健先生（左）
山崎塾 塾長　山崎幸子先生（右）
首都圏模試センター　三瓶勇美（本文※注監修）

場所：早稲田大学高等学院

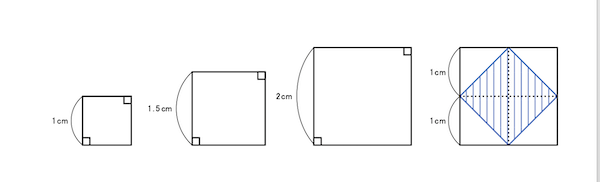
武沢：岡潔さん（1901-78。数学者）がお好きだと聞いたので、いろいろな本を持ってきました。数学に対する姿勢が、我々アジア人とギリシア人で違うお話をしましょう。『メノン』（プラトン）が好きで、今日のためにもう一度読み直してきました。「何であるか知らないものをどうやって探求することができるのか。そもそも知らないものの中から、どのようなものを探求の対象に選ぶことができるのか。また、もし探り当てたとしても、それが自分が知らなかったものだと、どうして知ることができるのか」ということが書かれています。「探求という言葉が頻繁に出てくるんですよ。知っていることを探求するのは無意味なわけですよね。かといって、知らないことは探求できないんじゃないかということを、メノンがソクラテスに問うんです。「探求のパラドックス」というんだけど、そこでソクラテスはメノンの召使に、正方形を使って説明する。砂浜に正方形を描いて、「君、この正方形の面積を2倍にするにはどうしたらいい」というように対話していく。召使が「各辺を2倍にする」と答えますが、それでは元の正方形の面積の4倍になってしまうことがわかります。じゃあ、「2倍では大きすぎるから、1.5倍」とします。しかしそれでも元の正方形の面積の2.25倍となってしまいます。そこで、ソクラテスは元の正方形を4個並べて、「元の正方形の対角線を辺にした正方形」に召使が気づけるまでに持っていくんですよ。彼はこれで想起ということを言うけれど、それは、うまく問いを立てて、相手に問いかけることによって、知識がない相手にも知識が出てくるということの一つの実例を示していると言えます。僕はギリシア人が、こういうことに数学を使っているところがすごいなと思うんです。

平井・山崎：そうですね。
武沢：『エチカ』（スピノザ）では、神の存在を定義、定理で証明していくんですよ。数学の本じゃないですよ。日本には、明治以降、欧米から数学が入ってきたので、数学というと問題解法、すなわち数学ができる人間はよい大学に入れる、理系に行けるという風になってしまった。ギリシア人がものを考えるときには、常にユークリッド原論の、「仮定を立てて、こうであったらこう。こうでなかったらこうだ」っていう、なんていうか癖があるんじゃないかなと、プラトンを読むたびに思います。
平井：岡潔さんも、同じようなことを言っていましたね。「与えるべきは問いだ」って。
武沢：書いてありましたよね。今、ChatGPTのような生成AIについていろんなこと言ってるけれど、うまく使うか使わないかは、問いにかかってくるじゃないですか。ソクラテスは産婆術、産むための手助けって言うんだけど、AIの時代といっても本質は同じじゃないかなという気がするんです。やっぱり基本はユークリッドの原論をモデルにしてると思うんですよね。
平井：公理（証明がなくても自明の真理となる根本命題）から始まり、定義と定理とは何かを相手に誤解のないように言葉で演繹的に説明する上で、どうしても必要な手法なのかもしれないですね。

武沢：プラトンは、仮説を立てて議論をすることが重要で、そのことは、ユークリッド原論が一つのモデルだという話をするんです。メノンでも、「徳とは誰が教えるものなのか」とか、「徳は訓練によって身につくものなのか」という問いかけから始まりますが、ソクラテスはまず「徳の本質的な定義を明確にしよう」と考える。これは、やはり数学的。それは無意識でやっているはずなんです。
平井：無意識ですね。「こう仮定したらどうなるのか？」、考え方は背理法と同じですね^※1。背理法は授業で学んでいない中学生でも、使えるんですよ。それを難しく背理法って言葉なんかで説明してしまうので、何だか難しそうとなったり、「いやこれはまだ高校生で習うから今は知らなくていいよ」としてしまったり。もっと素直な思考法で十分やれるんですよね。
武沢：子どもが積み木で遊ぶようなときでも、こうしたらどうだろうかと無意識でやっているはずですね。それがちゃんと言語化できるかが次のステップですよね。
※1:背理法（reductio ad absurdum）矛盾による証明

平井：そうですね。体験的に学ぶというのは、どうしても時間がかかったり、もしかすると間違った方法で学んでしまうかもしれないと言われますけれども、数学においては正直、その「間違った方法」っていうのがあまりなくて、後から整えればいいじゃないかと思っています。数学というものが完成してあるわけではなく、自分の中で数学的活動をしていること、「数学する」ということが一番大事なんだと思うんです。どうしたら相手によく伝わるかという発想自体も数学的だから、もっと体験的にそういう活動ができればいいなとは思います。
武沢：おそらく、部活動や学級活動などの意思決定においても、そういう思考法をきちんと身につけるかつけないかってことでしょうね。
平井：数学は解が一つしかないように思われるかもしれないのですけれど、先ほどの徳の話でいくと、「誠実である」とか「相手に対してもフェアな精神である」とか、「なるべく多くの人が納得いくような最適解」だったりしますが、部活動などでどうやったら民主的に合意形成できるかっていうプロセスには、極めて数学的な営みがあるような気がします。数学を真摯にやり続けることが、もしかしたら徳につながるのかなと感じます。

武沢：数学が高校、大学の受験科目になっているのは日本の教育の問題ですが、本来的には数学そのものは日常的なものですね。例えばおでんの中の大根について「君たちは円柱が入ってると言うけれど、大根って本来複雑な形でしょ。あれ実はね、微分して料理してるんだよ」って生徒に話すのだけど、区分求積をやってるわけですよね。お刺身、切り身なんていうのは区分求積法のピースです。
平井：江戸時代の和算ありますね。今も神社とかで算額（和算の絵馬）が飾られていますけれども、民衆にも広まっているのは、当時の日本人に「和算の面白さ」を感じる精神性があったわけですよね。和算ですごいものを見つけた時に何かしらの神秘性を彼らは感じて、神社に捧げるものだというふうに。日本人の感受性は高かったのかなと改めて思います。古い日本の建造物を見ると「何だかきれいだね」と感じる心をとても大事にしているような気がします。
武沢：そうなんですよね、法隆寺の五重塔とか正倉院の校倉造りなどは、あの時代に、あれだけのものを作ったということは、現代のような技術力、数学がなくても、根底にあるようなもので作ったのでしょうね、おそらく。それはすごい。
平井：西暦600年頃には計算式とかはなかったわけですよね。だけど、こうしたら崩れるとか、屋根はこう積み上げるとか、そういったところに関しても、当時の技術力や算数・数学の知識でよく作れたなと思いますね。
武沢：それを意識的に考えたのは丹下健三だと思います。東京の国立代々木競技場の吊り屋根は計算を駆使してやったのだろうけど、おそらく古代の建築なんかも勉強してたでしょうね。

平井：先ほど出た、何かしら根底にあるものっていうのが、岡潔さんが数学こそ情緒が大事だって言ったことにつながってくるのかなというふうに思います。
武沢：岡潔さんといえば『春宵十話』。
平井：私も最初の出会いは『春宵十話』でした。本当に名著ですね。惹かれて本屋行ったら『人間の建設』があって、小林英雄とも対談してたのかとびっくり。
山崎：自分も大好きです。何度も読みました。
武沢：彼はやはり日本人という意識が強いですね。よくわかります。西洋はインスピレーションだけど東洋は情緒だって断言している。広中平祐さん（1931-。数学者）の『学問の発見 数学者が語る「考えること・学ぶこと」』 も持ってきました。彼がハーバード大学の留学から帰ってきたときに発表したら岡さんに「君のやり方じゃうまくいかない」ってコテンパンにやられて非常に落ち込んだっていう話も出てくるんだけど。昔から読んでるけど、おもしろいですね。
山崎：矢野健太郎さん（1912-93。数学者）も好きです。新しい本が出るとすぐに買っていました。中学生の時、授業中に読んでて職員室に連れて行かれました。『すばらしい数学者たち』『解法の手引き』『モノグラフシリーズ』…、本棚いっぱいにあります。私が小中学生の頃にテレビに出ていらしたのが、きっかけなんじゃないかなと思います。
武沢：矢野さんの本も持ってくれば良かったな。去年、『学院雑誌』（校内誌）で、矢野さんの『解法のテクニック』を紹介しました。数学者は文章を書くのが上手ですよね。

平井：『人間の建設』にも無明という言葉がありましたね
武沢：僕も無明のところに付箋貼ってあります。
平井：それをどう説明したらいいか難しいですけど、あるがままっていうか…。
武沢：あの対談では小林秀雄さんの方がタジタジでしたね。数学の先生方も、もう少しゆとりがあればね、いろいろなことができるでしょう。うちの学校は大学受験を必要としないから教員たちも比較的好きなことはできます。
平井：私も数学はただただ楽しいっていう授業を心がけるようにはしてます。今、授業で極限とか無限の話をしてるんですけど、「アキレスと亀のパラドックス^※2」の話をしたら、生徒は“もやついて”いました。でも答えは教えていません。いつかどこかでわかればいいんじゃないないか、と思います。
武沢：本当は、ああいう話題が教科書に入ればいいですよね。

平井：教科書って問いかけたまま終われないことにとらわれているんじゃないでしょうか。問いだけでいいじゃないかって思っちゃうんですけど。
武沢：数学が人間の能力を測る一つの物差しになっちゃって、数学ができることが、その人間≒能力が高いみたいな誤解を招く指標になっています。できるかできないかがはっきりしているからだけれども、それは数学の極限化された一面です。僕も去年の学院祭（文化祭）のときに招待授業で「無限と連続」をやったんですよ。
※2:アキレスと亀：古代ギリシャの哲学者ゼノンが唱えたパラドックスの1つ。足の速いアキレスが足の遅い亀を追いかけ、亀が出発した地点にアキレスが到着したとき、亀は少し前に進んでいる。さらに追いかけ亀がいた位置に到着したとき、亀はまた少し前に進んでいる。この後さらに追いかけて…、と繰り返しても、アキレスは亀に追いつくことができない。

市川：松崎優里さんというSF作家の書いた『異世界数学』に、「数学のおもしろさの真髄はロマンだ」というくだりがあります。この作品の主人公は、数学は点数がつくから嫌いになっているんです。
平井：本当はもっと自由なんですけどね。
山崎：今はなくなってしまいましたが、昔はジャポニカ学習帳にも数学者の話がありました。小学生くらいだとそこが入り口になりますね。なくしちゃいけないと思います。1から100までの和を工夫してサッと計算してお父さんを驚かせたガウスの話とか、ピタゴラスのエピソードも覚えてます。
平井：その数学者のエピソードには、心ときめきますね。
山崎：「微積」って言葉にすごく憧れがあって、すごいことなんだろうけどよくわからないまま本を読んでいたけど、初めて教科書に微積が出てきたとき嬉しかったんですよ。
武沢：いや僕もそうなんですよ。中学生の時に読んだ矢野さんの『数学の世界』に微積が出てきて、極限って何だろうなってずっと不思議だったんだけど、高校2年で習って、こういうことだったのかと感激したことを思い出しました。
山崎：感激しますよね。高校生で経験するのって大きいです。

（2）へ続く